You don’t need a map to reach a summit if you know the direction of the steepest ascent. That’s the idea behind the hill climbing algorithm in AI. It’s not glamorous or grand, but it’s practical, efficient, and often surprisingly effective. Rather than looking at every possibility, it simply checks what’s around, finds what’s better, and keeps climbing—literally and metaphorically.

Whether it's tuning a model’s parameters or solving a constraint problem, hill climbing is often the first method explored in artificial intelligence because of its simplicity and speed. But under that simplicity lies a smart and deliberate method.

The Core Concept Behind Hill Climbing

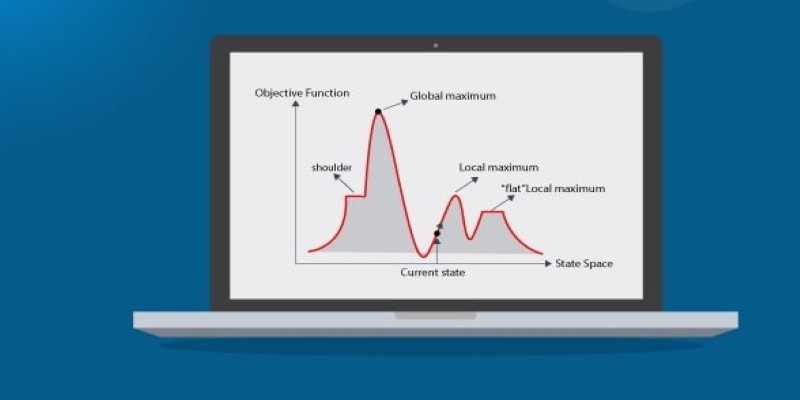
The hill climbing algorithm is a form of the local search algorithm. It is named "hill climbing" because it proceeds in the direction of rising value—such as walking up a hill—until it reaches the top. At every step, the algorithm checks neighboring solutions and selects the one with the optimal value based on a specific objective function. It repeats this process until there's no improvement to be found.

What makes this algorithm interesting is that it doesn’t keep a memory of past steps. It only cares about the current state and the best next move. That makes it greedy. It’s only concerned with immediate gain. And while that might sound shortsighted, it can be useful for a variety of problems where you don’t want or need to evaluate an entire solution space.

But being greedy comes with trade-offs. The algorithm can get stuck on local maxima, plateaus, or ridges. A local maximum is a point where all neighboring solutions are worse, even though a better global solution may exist elsewhere. A plateau is an area where all moves give the same result, leaving the algorithm unsure of where to go. Ridges are narrow paths where progress can only be made in a precise direction, which may not be apparent if only small steps are allowed.

Different Types of Hill Climbing

There are several variations of the hill climbing algorithm, each designed to overcome some of the common pitfalls. The simplest version is simple hill climbing, where the algorithm evaluates one neighboring state at a time and picks the first one that offers improvement. It's fast, but it might miss better paths that are just a few steps away.

Steepest ascent hill climbing is more thorough. It looks at all neighboring states and selects the one with the highest value. This method avoids taking smaller, less optimal steps but is more expensive because it evaluates more options in each round.

Stochastic hill climbing adds randomness. Instead of always picking the best immediate neighbor, it selects randomly among the better options. This randomness helps the algorithm escape local maxima by avoiding deterministic traps.

Finally, random-restart hill climbing takes things further. It runs the algorithm multiple times from different random starting points. This doesn't fix the greedy nature of each run, but it increases the chances that at least one run will find the global maximum. It’s like trying to reach the top of a mountain by starting from various places on the terrain.

Each variation makes the algorithm more flexible. Which one you choose depends on how smooth or rugged the solution space is and how much computational time you can afford.

Hill Climbing in Artificial Intelligence Problems

In artificial intelligence, hill climbing is used when the problem space is too large to examine exhaustively. It's common in optimization, feature selection, robotics, pathfinding, and game AI. The main idea is always the same: given a starting point, evaluate nearby states, move to the one that appears better, and repeat the process until no further improvement is possible.

Let's say you're tuning hyperparameters for a machine-learning model. Trying every possible combination can be time-consuming. Hill climbing offers a quick way to improve performance step by step. Even if it doesn't find the perfect combination, it often gets close enough—especially if combined with random restarts.

In-game AI is used for decision-making. The agent evaluates possible moves, picks the one with the best immediate result, and continues from there. It works well for simple games or situations where speed is more important than perfection.

In robotics, the hill climbing algorithm can help optimize movements or plan a path. The robot evaluates possible actions and picks the one that leads closer to the goal. Again, it doesn't guarantee the shortest or best path, but it usually finds a reasonable one quickly.

The same applies to constraint satisfaction problems, such as the N-Queens problem, where the goal is to place queens on a chessboard so that none threaten each other. Hill climbing helps by tweaking one queen at a time to reduce conflicts, moving toward a solution step by step.

What makes hill climbing fit so well in these areas is its balance between simplicity and performance. It doesn’t need extra memory or complex data structures. The focus is just on evaluating, choosing, and stepping forward.

Limitations and Workarounds

Hill climbing can be effective, but its short-sighted nature is a key weakness. It doesn’t account for long-term direction, making it prone to getting stuck in local optima. If it lands in a shallow dip that looks like a peak, it stops—even if a better hill is nearby.

To address this, variations such as stochastic or random-restart hill climbing reduce the likelihood of getting stuck. For more complex problems, AI systems often use simulated annealing or genetic algorithms, which are better at escaping local optima.

Another workaround is adjusting the neighborhood function. Instead of just small steps, the algorithm can take broader or more strategic moves. This improves its ability to navigate rugged solution spaces.

Despite these issues, hill climbing is still useful when a fast, lightweight optimization method is needed. It’s not perfect, but it’s often fast and reliable enough.

Conclusion

Hill climbing in AI is a local search algorithm that favors small, greedy steps toward better solutions without exploring every possibility. It's fast and simple but can get stuck in local optima since it lacks long-term vision. Variants like stochastic and random-restart versions help avoid these traps. Though not always the most accurate, its efficiency and low overhead make it useful for many practical AI problems where speed matters more than perfection.